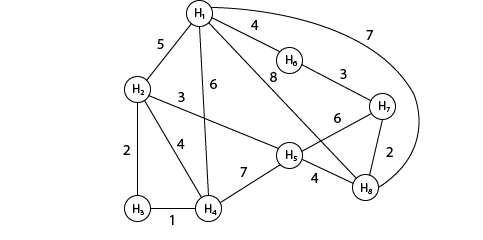
The traveling salesman problems abide by a salesman and a set of cities.
The salesman has to visit every one of the cities starting from a
certain one (e.g., the hometown) and to return to the same city.
The challenge of the problem is that the traveling salesman needs to
minimize the total length of the trip.
Suppose the cities are x1 x2..... xn where cost cij denotes the cost of
travelling from city xi to xj.
The travelling salesperson problem is to find a route starting and
ending at x1 that will take in all cities with the minimum cost.
Example: A newspaper agent daily drops the newspaper to the area
assigned in such a manner that he has to cover all the houses in the
respective area with minimum travel cost,
Compute the minimum travel cost.